Programmer Guide/SPU Reference/SPBCOEFS: Difference between revisions
m 1 revision: Initial import |
m moved Programmer Guide/SPU Reference/SPBCOEFS - compute spectral band coefficients to Programmer Guide/SPU Reference/SPBCOEFS |
(No difference)
| |
Latest revision as of 11:09, 28 April 2011
Contents
SPBCOEFS - compute spectral band coefficients
Usage:
SPBCOEFS x f f1 f2 n w r
Inputs:
| x | value vector (amplitude spectrum) | ||
| f | argument vector (frequency scale) | ||
| f1, f2 | integration range (must be inside the values of scale f) | ||
| n | number of integration coefficients (number of bands). This parameter is ignored if f1 and f2 are vectors. | ||
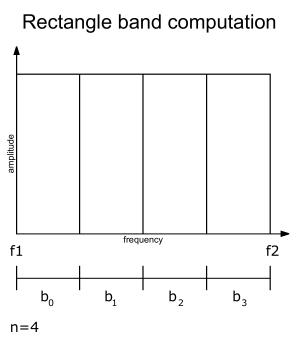
| w | type of integration window: | 'Rectangle' | (non overlapping) |
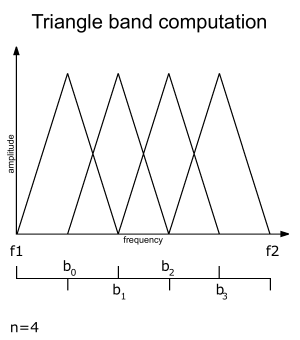
| 'Triangle' | (50% overlapping) | ||
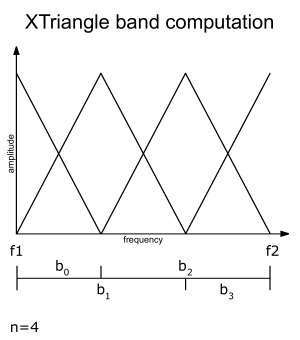
| 'XTriangle' | (50% overlapping, + last/first half window) | ||
| r | relative values (divide integration result by sum of integration weights) |
Outputs:
| y | integration coefficients |
Function:
Compute spectral band coefficients.
1) The frequency scale f must be in the same unit in which the bands should be equally spaced (E.g. to compute the Mel spectral coefficients, the scale must be transformed to Mel) and must have the same length as x.
2) f1 and f2 must use the same scale as f.
3) The frequency range is split into n bands. For every band i=0..n-1, a coefficient y[i] is calculated.
4) The calculation of the ith band bi for all n bands (i=0..n-1) depends on w:
| w = Rectangle | bi = (f2-f1)/n; band i is from f1+b*i to f1+b*i+b
|
| w = Triangle | bi = 2*(f2-f1)/(n+1); band i is from f1+b/2*i to f1+b/2*i+b
|
| w = XTriangle | bi = 2*(f2-f1)/(n-1); band 0 is from f1 to f1+b/2 (falling flank); band i (i = 1 .. n-2) is from f1+b/2*(i-1) to f1+b/2*(i-1)+b (complete triangle). band n-1 is from f2-b/2 to f2 (rising flank);
|
5) If r is 1 (On/Yes), the sum of the x values in a band is divided by the sum of the weightings (i.e. the area of the window function).
6) The inputs x and f are normally amplitude spectrum (linear, power or log) and a frequency scale (Hz, Mel, Bark etc.). Using x and f, the weighted sums can be computed for any function x(f).