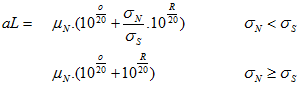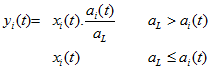DENOISE
Contents
DENOISE - noise reduction filter
Usage:
DENOISE1 X SR K O R S1 S2 N1 N2
Inputs:
| X | input signal |
| SR | sampling rate |
| K | time averaging factor |
| O | limiter offset in dB |
| R | limiter range in dB |
| S1,S2 | minimum and maximum frequency of signal band (in Hz) |
| N1,N2 | minimum and maximum frequency of noise band (in Hz) |
Outputs:
| Y | filtered signal (same type as X) |
Function:
This atom implements a noise reduction method. It was designed for the restoration of historical recordings with a limited bandwidth and a low dynamic range. The method was presented in a paper at the 75th AES convention in Paris (W.A. Deutsch, A. Noll: "Restoration of Historical Recordings").
First an average amplitude spectrum of the signal is computed using an exponential averaging method. The averaging is performed to reduce the statistical parts of the spectrum (noise) and to amplify the periodical parts (signal).
with:
x(t) amplitude spectrum at frame t a(t) average spectrum at frame t k averaging factor (time constant, 0 < k < 1)
In the second step, statistical values for the noise and signal band (defined by the frequencies S1..S2 and N1..N2) of the averaged spectrum a(t) are computed. These values and the limiter parameters R (range) and O (offset) are used to detect the presence of a signal and to compute the limiter value aL that controls the filter spectrum computation:
with: mS, sS average and variance of magnitudes in the signal band mN, sN average and variance of magnitudes in the noise band
In this signal detection method it is assumed that the distortion signal is a white noise. It may be necessary to use a pre-whitening filter (inverse spectrum of pauses) for compensation. This compensation can also be used to remove (reduce) influences of the (historical) recording system (e.g. resonance). The estimated aL is used in the 3rd step to generate the filter frequency response and apply it to the input spectrum x(t) to compute the (enthanced / denoised) output spectrum y(t).
with: h(t) filter magnitude response (spectrum) y(t) filtered spectrum t, i frame and frequency index
Notes
If no periodical parts are present in the signal, the ratio of sN/sS is near to 1. In this case the filter spectrum is set to: hi(t) = ai(t) / mN / amax with amax = (10O/20 + 10R/20). This leads to a reduction of noise-only parts of the input signal by the factor amax (because ai(t) » mN).
If the signal consists of weak periodical parts (in the signal band) and noise (in both bands) the ratio sN/sS is lower than 1. The filter spectrum is set to: hi(t) = ai(t) / mN / a with a = (10O/20 + sN/sS.10R/20). In this case the noise reduction factor is smaller that amax because a signal is present. Because the filter spectrum is a smoothed version of the signal spectrum, the magnitude relations are expanded (quadratic expansion).
If strong spectral components are also contained in the signal, the same filter spectrum computation as above is used, but hi(t) is set to 1 if ai(t) is larger than the limiter level aL (=mN . a). This limitation avoids the expansion of strong periodical components of the signal.
The average factor k can be interpreted as (or derived from) an averaging time constant. E.g. the following method can be used to get an estimation of k:
with: T time constant in seconds q part of x(t-T) in a(t) (0 < q << 1) D frame distance in seconds (e.g.: D=filterlength/2 for filters using half-overlapping)
e.g.: q = 10-3 (-60dB), T=0.5s, D=50ms -> k = (1 – 10-0.3)2 » 0.25