Frames and Finite Dimensionality:
Frame Transformation, Classification and Algorithms

created: 09/05/2006; last update: 03/12/2015

Update 2015:

The topic of frames in finite dimensional spaces is treated in much more details in

Eds. P.G. Casazza and G. Kutyniok, Finite Frames: Theory and Applications, Birkhäuser, Boston (2012)

The implementation for general frames can be found in

Zdeněk Průša, Peter L. Søndergaard, Nicki Holighaus, Christoph Wiesmeyr, Peter Balazs The Large Time-Frequency Analysis Toolbox 2.0. Sound, Music, and Motion, Lecture Notes in Computer Science 2014, pp 419-442

The frame concept is used in LTFAT with an object-oriented approach, see the documentation.

This webpage is linked to the paper

P. Balazs, "Frames and Finite Dimensionality: Frame Transformation, Classification and Algorithms", Applied Mathematical Sciences, Vol. 2, no. 41-44, pp. 2131-2144, (2008) (preprint on arxiv),

Codes (MATLAB):

Build the synthesis matrix for the canonical dual frame: candualframe(D)
Build the synthesis matrix for the canonical tight frame: cantightframe(D)
Cross-Gram Matrix of two sequences: CrossGram(D1,D2)
Calculate the framebounds of a frame: framebounds(D)
Create random frame (in the unit circle): RandFrame(dim,M)
Plot 2- and 3-dimensional frame: PlotFrame(D)
Script for testing the frame transformation using stochastic parameters: testframtrans2
Script for testing the frame transformation using fixed frames: testframtrans
Arrowline 2-D and 3-D vector plot allowing colors and annotations: vectarrowxxl(p0,p1) [based on external code vectarrow(p0,p1)].
All codes collected in one ZIP-file.

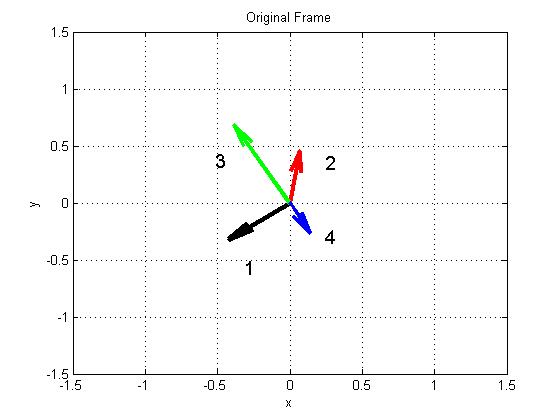
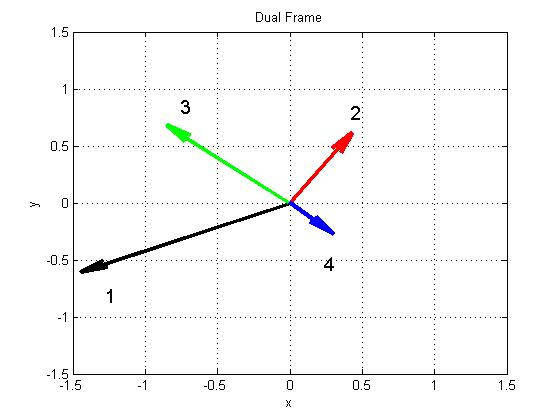
Representation of the vectors of the frame (left) and its dual (right) of Example 3.1
Representation of the vectors of the frame (left) and its dual (right) of Example 3.2
R
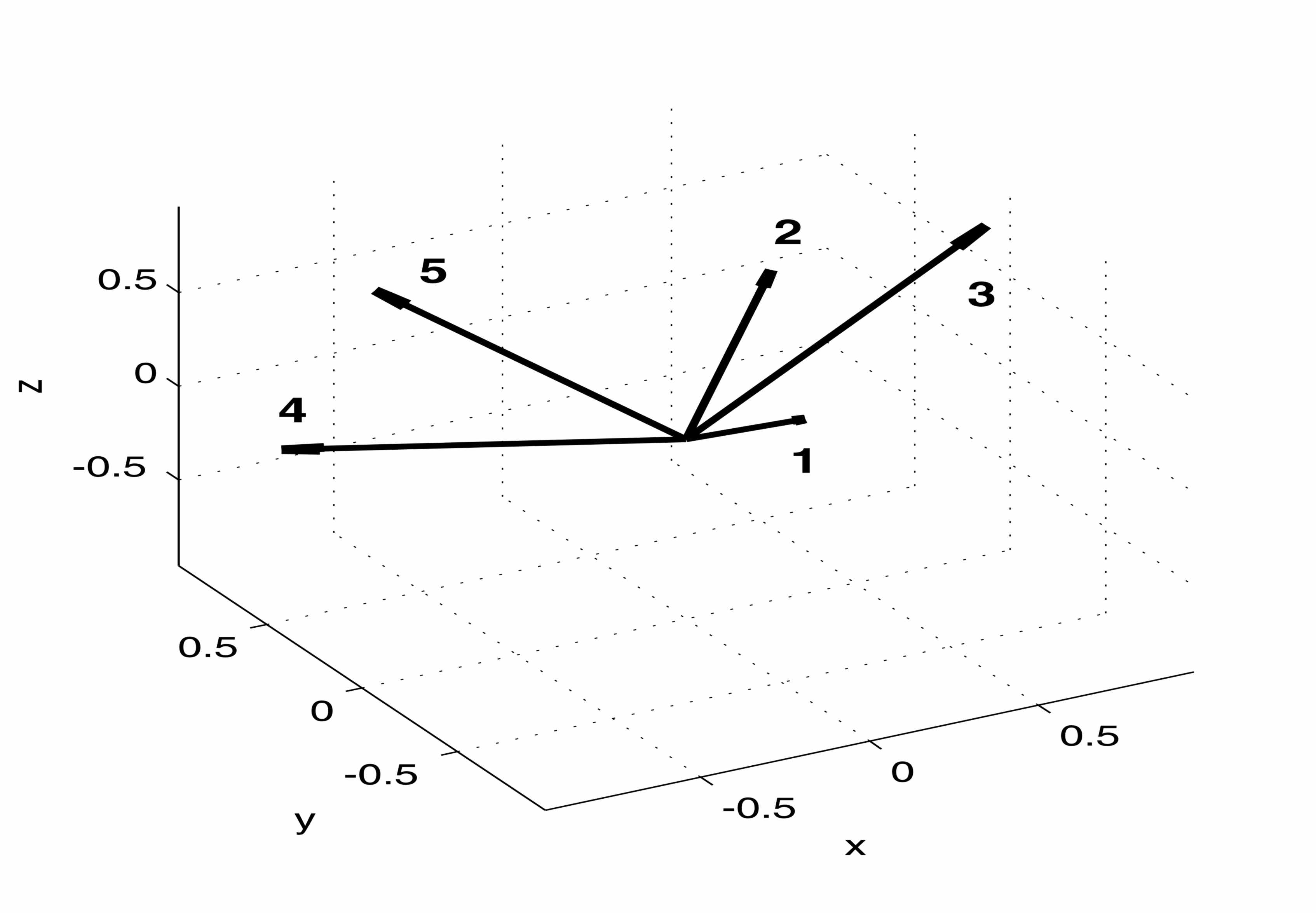
Representation of the vectors of the frame (left) and its dual (right) of Example 3.3 (numbers were manually added).